DH 是 Diffie-Hellman的首字母缩写,是Whitefield与Martin Hellman在1976年提出了一个的密钥协商协议。其安全性源于在有限域上计算离散对数。该算法可以使两个用户之间安全地交换一个密钥,但不能用于加密或解密信息。
原理:
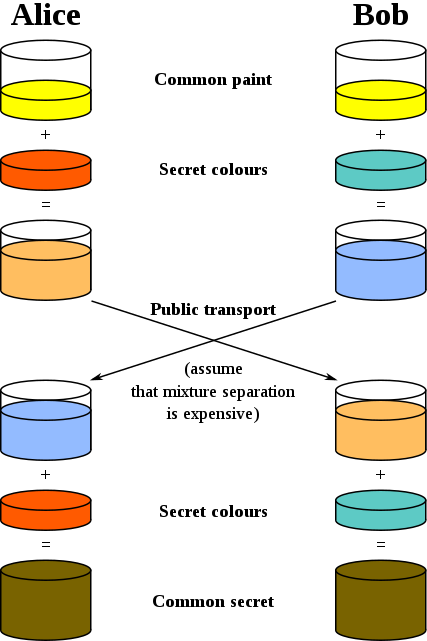
- Alice和Bob首先约定好公开的一种颜色,比如黄色
- Alice和Bob各自挑选出一种私密的颜色,比如橙色和青色
- Alice和Bob各自将两种颜色混合起来
- 双方交换混合后的颜色
- Alice和Bob各自将自己的私密颜色再次混入得到的颜色中
- 现在Alice和Bob得到了一种相同的颜色,这种颜色是由一份黄色、一份橙色、一份青色混合而来,但外界无法得知
颜色混合是一种“不可逆”的操作,当双方交换颜色时,尽管我们知道他们交换的颜色都是由一份黄色和另一份其他颜色混合得到的,但我们还是无法或者很难得到他们的私密颜色。而DH秘钥交换的原理非常相似,也是利用了数学上的一个“不可逆”的运算,就是离散对数
乘方得逆运算称为对数运算,比如已知
7^x = 49
那么可知
x = log7 49 = 2
对数运算非常容易,即使在数字很大的时候是,但如果是下面的情况
7^x mod 13 = 8
求X的过程称为“离散对数”,就不那么容易了,在数字很大时几乎是一个不可能的运算,而DH秘钥交换就是利用了这种离散对数计算非常困难的特性来设计的。
公式里的mod是取模运算,取模运算有几条基本的定律如下
(a+b) mod P = (a mod P + b mod P) mod P
(ab) mod P = (a mod P b mod P) mod P
(a^b) mod P = ((a mod P)^b) mod P
根据上面的公式,可以推导出一个非常重要的公式
(G^(a*b)) mod P = (G^a mod P)^b mod P = (G^b mod P)^a mod P
根据这个公式,我们可以向上面交换颜色那样设计出一个秘密交换数字的流程出来
A和B首先约定两个公开的质数 p 和 g
A和B各自随机产生两个数 a, b,作为自己的私钥
各自计算出自己的公钥 A, B
A = g^a mod p
B = g^b mod p
交换公钥 A, B
计算出加密用的密钥S
Sa=B^a mod p=(g^b mod p)^a mod p=g^(a*b) mod p
Sb=A^b mod p=(g^a mod p)^b mod p=g^(a*b) mod p
最终两个人得到的秘密数字都是 g^(ab) mod p,而窃听者仅从p, g, A, B四个公开信息,是无法得到这个秘密数字的
举个例子,假如 p=23,g=5,Alice选取的秘密数字 a=6,那么 A=5^6 mod 23=8,Bob选取的秘密数字是 b=15,那么 B=5^15 mod 23=19,交换A和B后,Alice计算出的密钥 Sa=19^6 mod 23=2,Bob计算出的密钥 Sb=8^15 mod 23=2
当然,实际运算中不可能取这么小的数值,比如如果需要128bit长度的密钥,那么p值需要是128bit长度的质数,由于有模运算,所获得的密钥不会大于p,所以p值可以是128bit数字中最大的一个质数,g可以随便设置一个小的质数即可。
缺点
如果注意的是,为了防止应用优化算法计算上述问题,质数p不是随便选择的,需要符合一定的条件。
随机数a、b的生成算法也必需注意,应使结果尽可能随机,不能出现可预测的规律,否则会使破解变的容易。
通过上述计算过程也可以看出DH算法不仅可以应用在2方通信的情况,如果多方通信,也可以使用该算法。
DH密钥交换算法无法验证对方身份,所以DH密钥交换算法不能抵御中间人攻击
DH算法中间人攻击原理:
从其原理之中可以看出,a,b 值并没有什么关系,a,b不能证明通信双方Alice与Bob的身份,这使得重放攻击可以轻易产生。
假设一个攻击者 Tom,当 Alice 向 Bob 发送 g, p, A 时,Tom 截获了信息,并(假装自己是 Bob)向 Alice 发送了 T=g^t mod p,其中 t 是 Tom 的私钥。同时 Tom(假装自己是 Alice)向 Bob 发送 g,p,T=g^t mod p,这样 Bob 以为这是 Alice 发过来的,就向 T 发送了 B=g^b mod p。
在 Alice 与 Tom 之间,创建的密钥就是 Sta=g^at mod p,两方密钥相同。
在 Tom 与 Bob 之间,创建的密钥就是 Stb=g^tb mod p,两方密钥相同。
这样,密钥创建完成,Alice 与 Bob 都认为自己与对方分享了只有他们两人所知的密钥,实际上并不是。当 Alice 想要发信息给 Bob 时,Alice 就会将信息用 Sta=g^at mod p 加密后发出,消息 Bob 无法解密,但会被 Tom 收到并解密,这样 Tom 可以或者扣留信息,或者篡改信息用 Stb=g^tb mod p 加密后发给 Bob,这样 Bob 会收到他认为是 Alice 发来的,其实是 Tom 发过来的经过篡改的信息。这样重放攻击就产生了。
解决:
可以采用数据签名技术解决中DH密钥交换过程中可能存在的中间人攻击
参考链接
链接: