平方乘算法
RSA 加解密中存在指数运算 X^a。通常解密运算中的指数非常大,a 的二进制位数通常会大于等于1024 bit,即可能 a >= 2^1024。如果用一般方法直接计算 X^a 的值, 即 X*X*X……需要的运算量非常大,很容易溢出。
定义:MUL 为乘法运算即乘以 X,sq 为平方运算
考虑一个例子计算 X^8,则最简单的方法需要8次乘法运算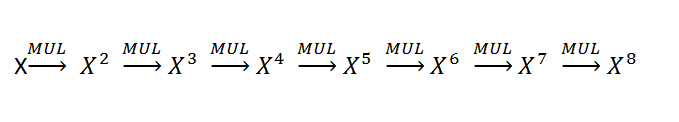
而更快捷的方法只需要3次平方运算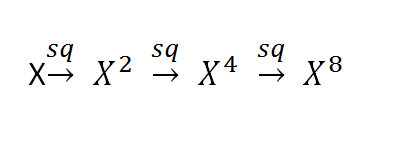
在看一个更一般的例子,计算 X^24,最简单的方法就是计算24次乘法。
更有效的方法如下:即一次平方操作,一次乘法操作(乘以 X),之后再三次平放操作。 即5次操作即可得到结果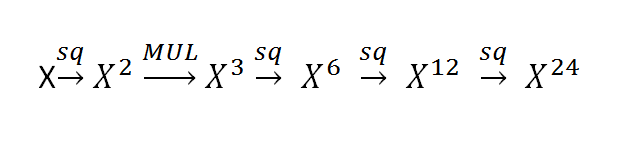
也就是说对于指数运算两种基本操作就可以得到结果:对当前结果平方,当前结果与 X 相乘。问题是如何确定平方与乘法的执行顺序, 平方-乘算法就可以解决这个问题。
大致描述为: 对 X^a 将指数 a 表示为2进制形式,高bit在左,然后从左至右扫描对应的 bit 位。除了最左边的 bit(MSB)以外,在扫描之后每个 bit 位时对当前结果平方,如果该bit位为1,则需多进行一次乘法操作
以计算 X^24 为例:
黑体表示二进制形式
X^24 将指数表示为二进制形式 X^11000 表示为 X^b1b2b3b4b5
开始扫描指数的每个Bit:
- 初始值 X = X^1; 初始化设置,b1 = 1,扫描第一个bit时不需要做其他操作
- X^2 = X^11 b2=1,先平方 X^2*X = X^3 = X11 ,再乘以 X
- (X^3)^2 = X^6 = X^110 b3= 0,只需要一次平方
- (X^6)^2 = X^12 = X^1100 b4 = 0,只需要一次平方
- (X^12)^2 = X^24 = X^11000 b5 = 0,只需一次平方
通过观察运算过程中指数的二进制表示的变化能更好的理解算法,一次平方操作会让指数向左移一位,并在最右边添加0,
而与 X 相乘的操作即在指数的最右边位置上填上 1
快速幂算法
所谓的快速幂,实际上是快速幂取模的缩写,简单的说,就是快速的求一个幂式的模(余)。在程序设计过程中,经常要去求一些大数对于某个数的余数,为了得到更快、计算范围更大的算法,产生了快速幂取模算法。
快速幂实现基于引理:积的取余等于取余的积的取余,即:
(a * b) mod n=(a mod n * b mod n) mod n
示例:4^24 mod 102 = 52
24 = 11000
4^24 mod 102 = ( ( ( ( (4^1)*(4^1)^2 ) ^2) ^2) ^2) mod 102
= ( ( ( 64 ^2) ^2) ^2) mod 102
= ( ( ( 64 ^2) ^2) mod 102) ^2 mod 102
= ( ( ( 64 ^2) mod 102)^2 mod 102) ^2 mod 102
= ( ( 256 mod 102)^2 mod 102) ^2 mod 102
= ( 52^2 mod 102) ^2 mod 102
= ( 52^2) mod 102
= 52